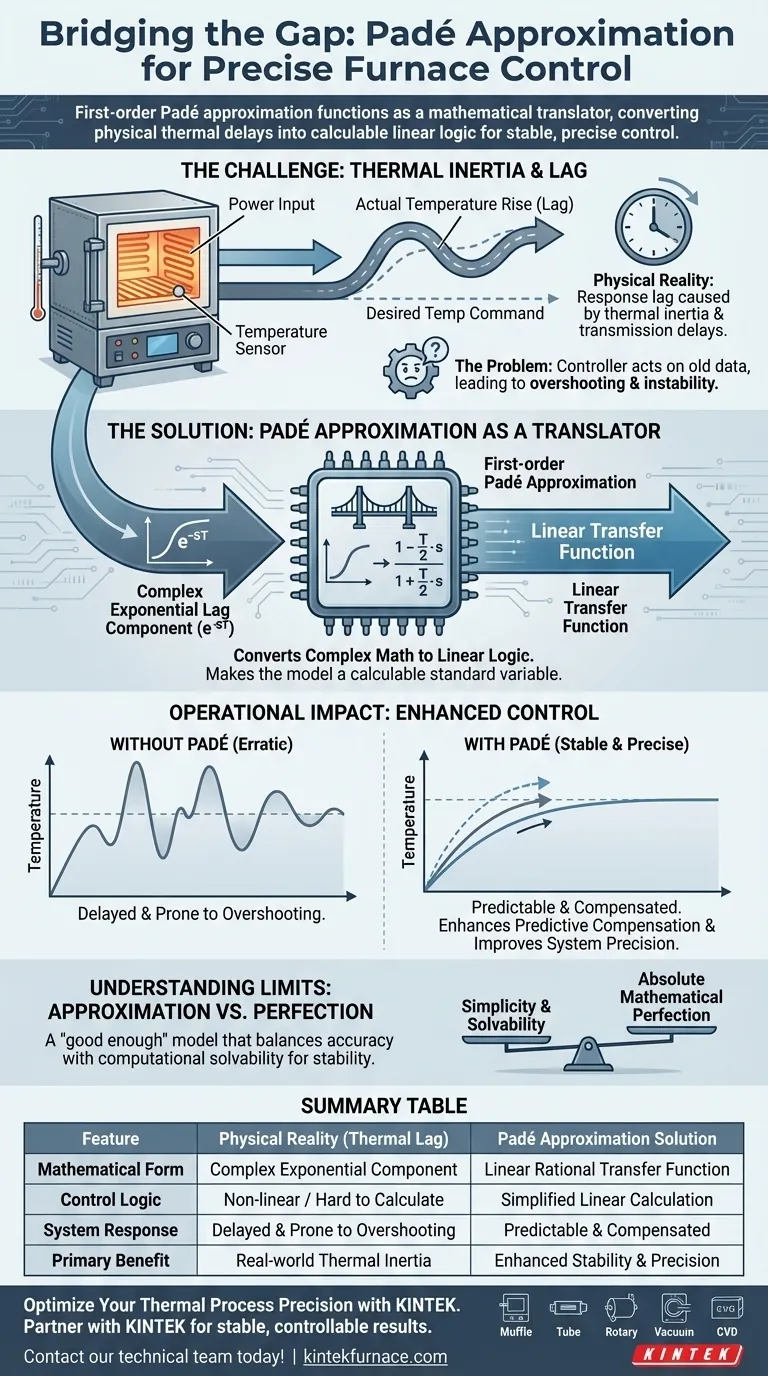
La aproximación de Padé de primer orden funciona como un traductor matemático que une la brecha entre los retrasos térmicos físicos y la lógica del sistema de control. Aborda los desafíos técnicos en la regulación de hornos eléctricos al convertir componentes complejos de retardo exponencial, causados por la inercia térmica y los retrasos de transmisión, en una función de transferencia lineal calculable. Esta transformación permite al controlador compensar eficazmente los retrasos de respuesta, asegurando que el sistema permanezca estable y preciso.
Los hornos eléctricos industriales poseen una inercia térmica significativa, lo que crea retardos de tiempo difíciles de gestionar para los algoritmos estándar. La aproximación de Padé de primer orden simplifica estos retardos complejos en un formato lineal, lo que permite al sistema de control predecir el comportamiento de manera confiable y mantener una regulación precisa de la temperatura.
El Desafío: Inercia Térmica y Retardo
La Realidad Física de los Hornos Eléctricos
En entornos industriales, los hornos eléctricos no responden instantáneamente a los cambios de potencia. Siempre hay un retraso de respuesta causado por la inercia térmica y los retrasos de transmisión.
El Problema de los Retardos de Tiempo
Cuando un controlador envía una señal para aumentar el calor, el aumento real de la temperatura ocurre más tarde. Este retraso de transmisión crea una desconexión entre el comando y el resultado.
Sin un modelado adecuado, un controlador reacciona a datos antiguos. Esto a menudo conduce a sobrepasar la temperatura objetivo o a la inestabilidad del sistema.
Cómo la Aproximación de Padé Resuelve el Problema
Convirtiendo Matemáticas Complejas en Lógica Lineal
Matemáticamente, los retardos de tiempo puros se representan como componentes complejos de retardo exponencial. Estos son difíciles de usar directamente en los cálculos estándar del bucle de control lineal.
La aproximación de Padé de primer orden resuelve esto al convertir el término exponencial en una función de transferencia lineal. Crea una fracción racional matemática que aproxima el retardo.
Haciendo el Modelo Calculable
Una vez convertido, el retardo se convierte en una parte manejable de la ecuación del sistema. El algoritmo de control ahora puede procesar el retardo como una variable estándar en lugar de una anomalía compleja.
Impacto Operacional en el Control de Temperatura
Mejora de la Compensación Predictiva
Al linealizar el retardo, el controlador del horno puede predecir de manera más confiable cómo reaccionará la temperatura con el tiempo. Puede "ver" el retardo que se aproxima y ajustar la potencia de salida con anticipación para compensar.
Mejora de la Precisión y Estabilidad del Sistema
El resultado final es un sistema más robusto. Debido a que el controlador tiene en cuenta la inercia térmica con precisión, evita fluctuaciones erráticas.
Esto conduce a una mayor precisión y estabilidad durante la operación real, asegurando que el horno mantenga la temperatura correcta sin oscilaciones constantes.
Comprendiendo los Límites de la Aproximación
Aproximación vs. Perfección
Es importante recordar que este método es una aproximación, no una réplica exacta del retardo físico. Simplifica la serie infinita de una función exponencial en una relación lineal finita.
Equilibrio entre Simplicidad y Precisión
Si bien es muy eficaz para estabilizar bucles de hornos estándar, sacrifica la perfección matemática absoluta por la resolución computacional. Proporciona un modelo que es "suficientemente bueno" para garantizar la estabilidad sin requerir una potencia de procesamiento excesiva.
Tomando la Decisión Correcta para su Estrategia de Control
Al diseñar o ajustar un modelo de control de temperatura para un horno eléctrico, considere cómo esta aproximación se alinea con sus objetivos específicos.
- Si su enfoque principal es la Estabilidad del Sistema: Utilice la aproximación de Padé para evitar oscilaciones causadas por el retardo entre el elemento calefactor y el sensor.
- Si su enfoque principal es la Simplicidad del Algoritmo: Implemente este método para convertir matemáticas de retardo no lineal complejas en una función lineal estándar fácil de calcular.
Al convertir el retardo físico en un valor matemático lineal, transforma una respuesta térmica caótica en un proceso predecible y controlable.
Tabla Resumen:
| Característica | Realidad Física (Retardo Térmico) | Solución de Aproximación de Padé |
|---|---|---|
| Forma Matemática | Componente Exponencial Complejo | Función de Transferencia Racional Lineal |
| Lógica de Control | No Lineal / Difícil de Calcular | Cálculo Lineal Simplificado |
| Respuesta del Sistema | Retrasada y Propensa a Sobrepasarse | Predecible y Compensada |
| Beneficio Principal | Inercia Térmica del Mundo Real | Estabilidad y Precisión Mejoradas |
Optimice la Precisión de su Proceso Térmico con KINTEK
Superar la inercia térmica requiere tanto precisión matemática como hardware de alto rendimiento. KINTEK ofrece soluciones de calefacción líderes en la industria respaldadas por I+D y fabricación expertas. Ya sea que necesite sistemas Muffle, Tube, Rotary, Vacuum o CVD, nuestros hornos de alta temperatura de laboratorio son totalmente personalizables para satisfacer sus necesidades únicas de regulación de temperatura.
No permita que los retardos de respuesta comprometan sus resultados. Asóciese con KINTEK para lograr la estabilidad y el control que exige su investigación. ¡Contacte a nuestro equipo técnico hoy mismo para discutir los requisitos de su horno personalizado!
Guía Visual
Referencias
- Serdar Ekinci, Євген Зайцев. Efficient control strategy for electric furnace temperature regulation using quadratic interpolation optimization. DOI: 10.1038/s41598-024-84085-w
Este artículo también se basa en información técnica de Kintek Furnace Base de Conocimientos .
Productos relacionados
- 1200℃ Horno de atmósfera inerte de nitrógeno controlada
- 1700℃ Horno de atmósfera de nitrógeno inerte controlada
- 1400℃ Horno de atmósfera de nitrógeno inerte controlada
- 1200℃ Horno de tubo partido Horno de tubo de cuarzo de laboratorio con tubo de cuarzo
- Horno de sinterización por plasma SPS
La gente también pregunta
- ¿Cómo funciona el tratamiento térmico en atmósfera inerte? Prevención de la oxidación para una calidad de material superior
- ¿Cuál es el propósito principal del tratamiento térmico? Transformar las propiedades del metal para un rendimiento superior
- ¿Cuáles son los beneficios del tratamiento térmico en atmósfera inerte? Prevenir la oxidación y preservar la integridad del material
- ¿Qué industrias utilizan comúnmente el tratamiento térmico en atmósfera inerte? Aplicaciones clave en el sector militar, automotriz y más
- ¿Para qué se utiliza el nitrógeno en un horno? Prevenir la oxidación y controlar la calidad del tratamiento térmico
